Day 16 of 100 Days of Dsa Challenge

Today, I tackled the K-th Symbol in a Grammar problem on LeetCode. Initially, I approached the problem by using a binary string, but consistently faced "memory limit exceeded" issues. Despite spending around 2 hours attempting to optimize my code, I couldn't resolve the problem. Eventually, I decided to explore a solution on YouTube. Surprisingly, the logic presented in the video was identical to mine, but they employed a different approach without using a binary string.

Here's my initial code:

class Solution {
public:
    string negate_1(string str){
        for(int i=0;i<str.size();i++){
            if(str[i]=='0'){
                str[i] = '1';
            }else{
                str[i] = '0';
            }
        }
        return str;
    }

    string ans(int n){
        //base case
        if(n ==1){
            return "0";
        }
        return ans(n-1) + negate_1(ans(n-1));
    }

    int kthGrammar(int n, int k) {
        string solution = ans(n);
        return solution[k-1]-'0';
    }
};

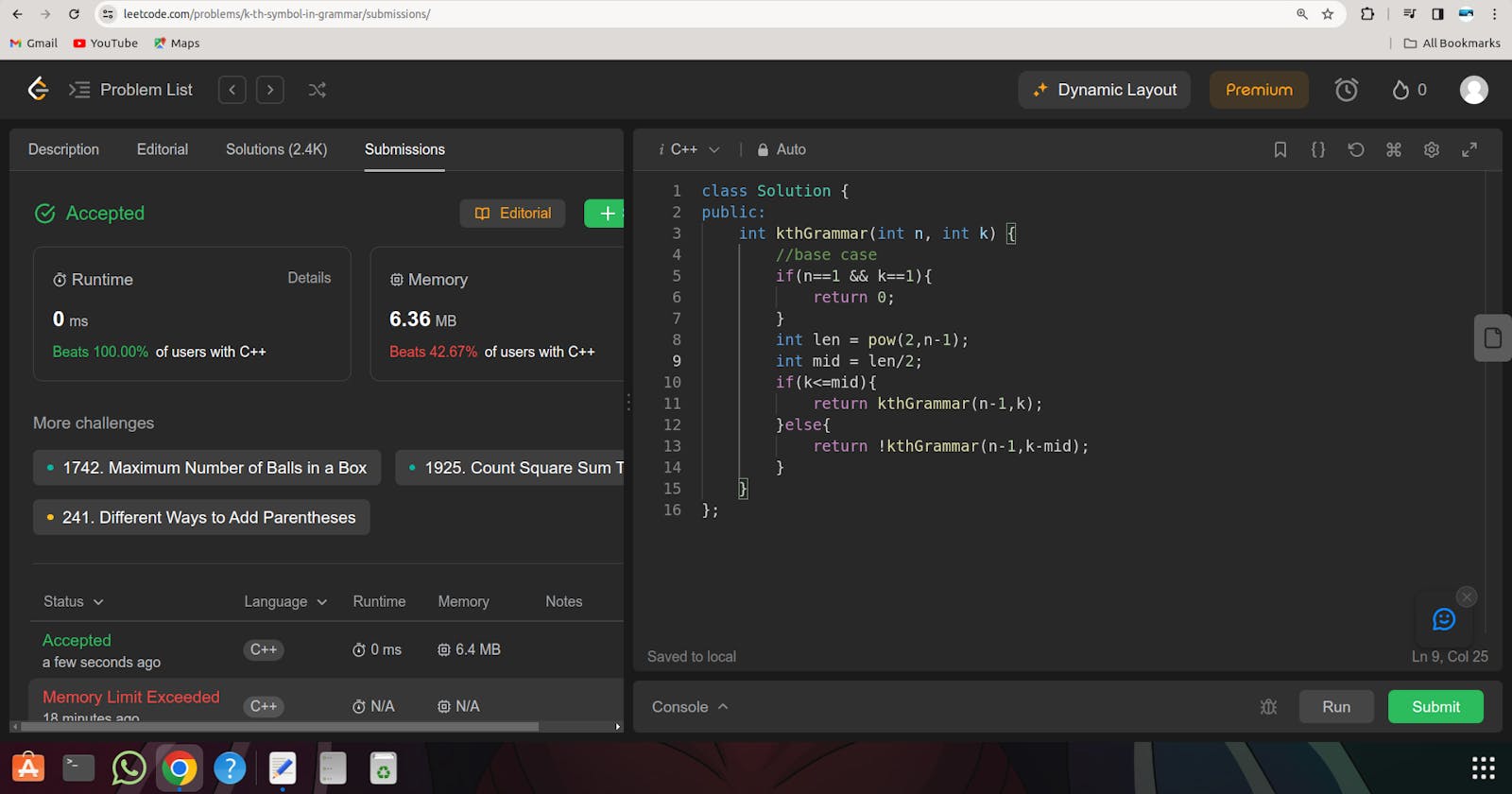
After researching, I discovered a more optimized approach. The key logic remained the same, but the implementation became more concise:

class Solution {
public:
    int kthGrammar(int n, int k) {
        //base case
        if(n == 1 && k == 1){
            return 0;
        }
        int len = pow(2, n - 1);
        int mid = len / 2;
        if(k <= mid){
            return kthGrammar(n - 1, k);
        } else {
            return !kthGrammar(n - 1, k - mid);
        }
    }
};

By comparing the two versions, it's evident that the optimized solution is not only more concise but also avoids the memory issues encountered in the initial attempt. This experience highlighted the importance of not only developing a sound logic for a problem but also optimizing the code for efficiency.