Day 8 of my 100 Days of DSA Challenge: Exploring Merge Sort in C++

Hey there, fellow learners! It's Day 8 of my 100 Days of Data Structures and Algorithms (DSA) challenge, and today I delved into the world of Merge Sort. I've got a simple and effective C++ implementation to share with you.

Understanding Merge Sort

Merge Sort is a popular sorting algorithm known for its efficiency. It's a "divide and conquer" algorithm that divides the array into smaller parts until they become trivially sortable (single elements), then merges them back together in a sorted order.

Explaining the Code

Let's break down the C++ code to implement Merge Sort:

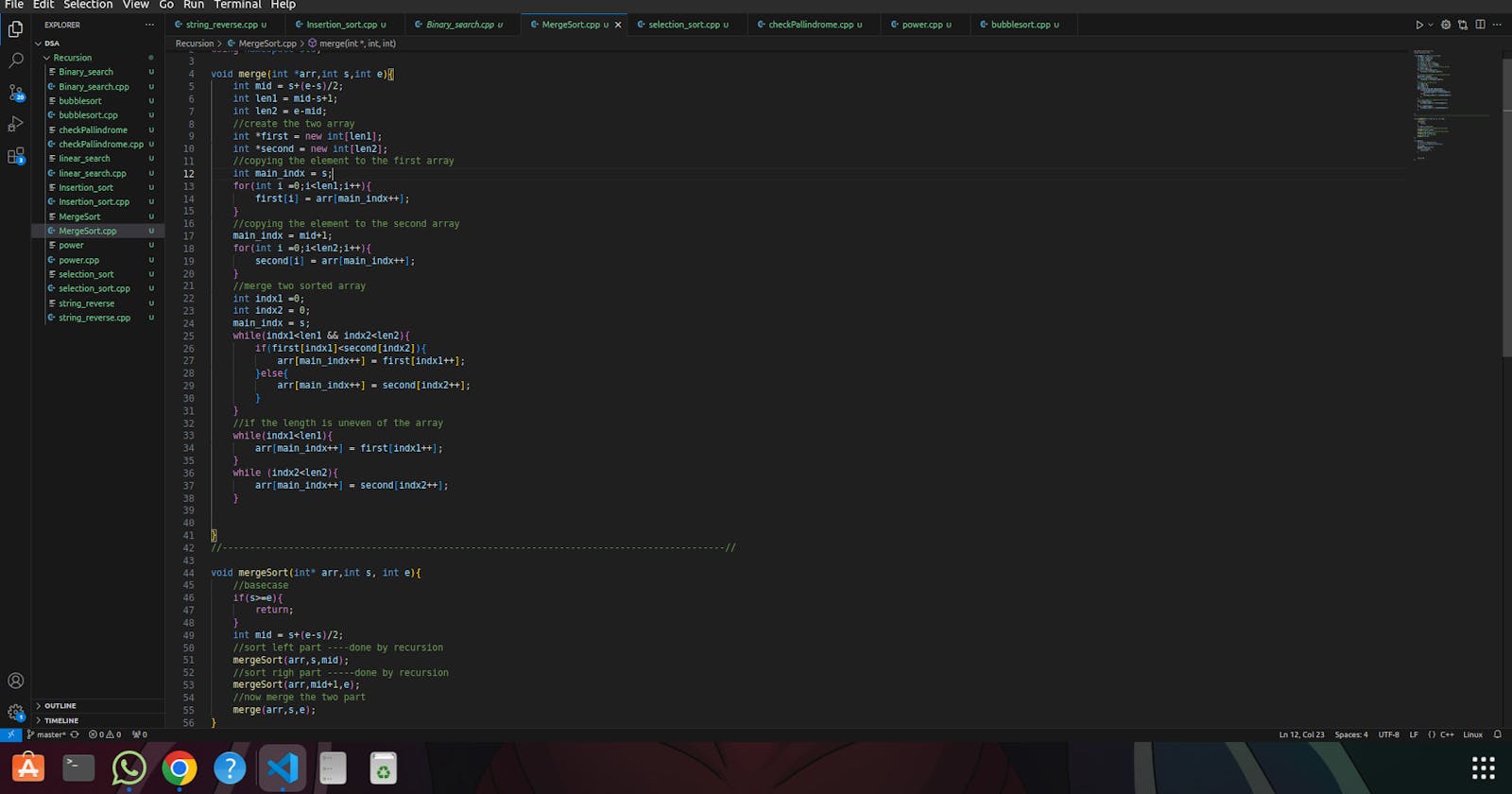
#include <bits/stdc++.h>
using namespace std;
//tie-------------------------------------->
void merge(int *arr,int s,int e){
    int mid = s+(e-s)/2;
    int len1 = mid-s+1;
    int len2 = e-mid;
    //create the two array
    int *first = new int[len1];
    int *second = new int[len2];
    //copying the element to the first array
    int main_indx = s;
    for(int i =0;i<len1;i++){
        first[i] = arr[main_indx++];
    }
    //copying the element to the second array
    main_indx = mid+1;
    for(int i =0;i<len2;i++){
        second[i] = arr[main_indx++];
    }
    //merge two sorted array
    int indx1 =0;
    int indx2 = 0;
    main_indx = s;
    while(indx1<len1 && indx2<len2){
        if(first[indx1]<second[indx2]){
            arr[main_indx++] = first[indx1++];
        }else{
            arr[main_indx++] = second[indx2++];
        }
    }
    //if the length is uneven of the array
    while(indx1<len1){
        arr[main_indx++] = first[indx1++];
    }
    while (indx2<len2){
        arr[main_indx++] = second[indx2++];
    }


}
//-------------------------------------------------------------------------------------------//

void mergeSort(int* arr,int s, int e){
    //basecase
    if(s>=e){
        return;
    }
    int mid = s+(e-s)/2;
    //sort left part ----done by recursion
    mergeSort(arr,s,mid);
    //sort righ part -----done by recursion
    mergeSort(arr,mid+1,e);
    //now merge the two part
    merge(arr,s,e);
}

int main(){
    int arr[] = {5,4,3,7,1};
    int n = sizeof(arr)/sizeof(int);
    int s =0;
    mergeSort(arr,s,n-1);
    for(int it:arr){
        cout<<it<<" ";
    }



    return 0;
}
//take it easy---------------------------------------->

Key Functions

1. merge Function:

   • This function merges two sorted arrays.

   • It creates two temporary arrays and copies elements into them.

   • Then, it merges these arrays back into the original array in a sorted order.

2. mergeSort Function:

   • A recursive function that sorts the array by dividing it into smaller halves until they're individually sorted.

   • Then, it starts merging these sorted parts back together using the merge function.

3. main Function:

   • Initializes an array with some values.

   • Calls the mergeSort function to sort the array.

   • Prints the sorted array.

Step-by-Step Execution

1. The mergeSort function recursively divides the array into smaller parts.

2. Once it reaches individual elements, it starts merging them in a sorted order using the merge function.

3. Finally, the main function outputs the sorted array.

Conclusion

This implementation efficiently sorts the given array using the Merge Sort algorithm by recursively dividing the array into smaller halves and merging them in a sorted manner.

That's the beauty of Merge Sort—efficient, easy to understand, and a powerful algorithm for sorting. Stay tuned for Day 9, where I'll dive into another fascinating concept in the realm of DSA!

Happy coding! 🚀✨