Introduction

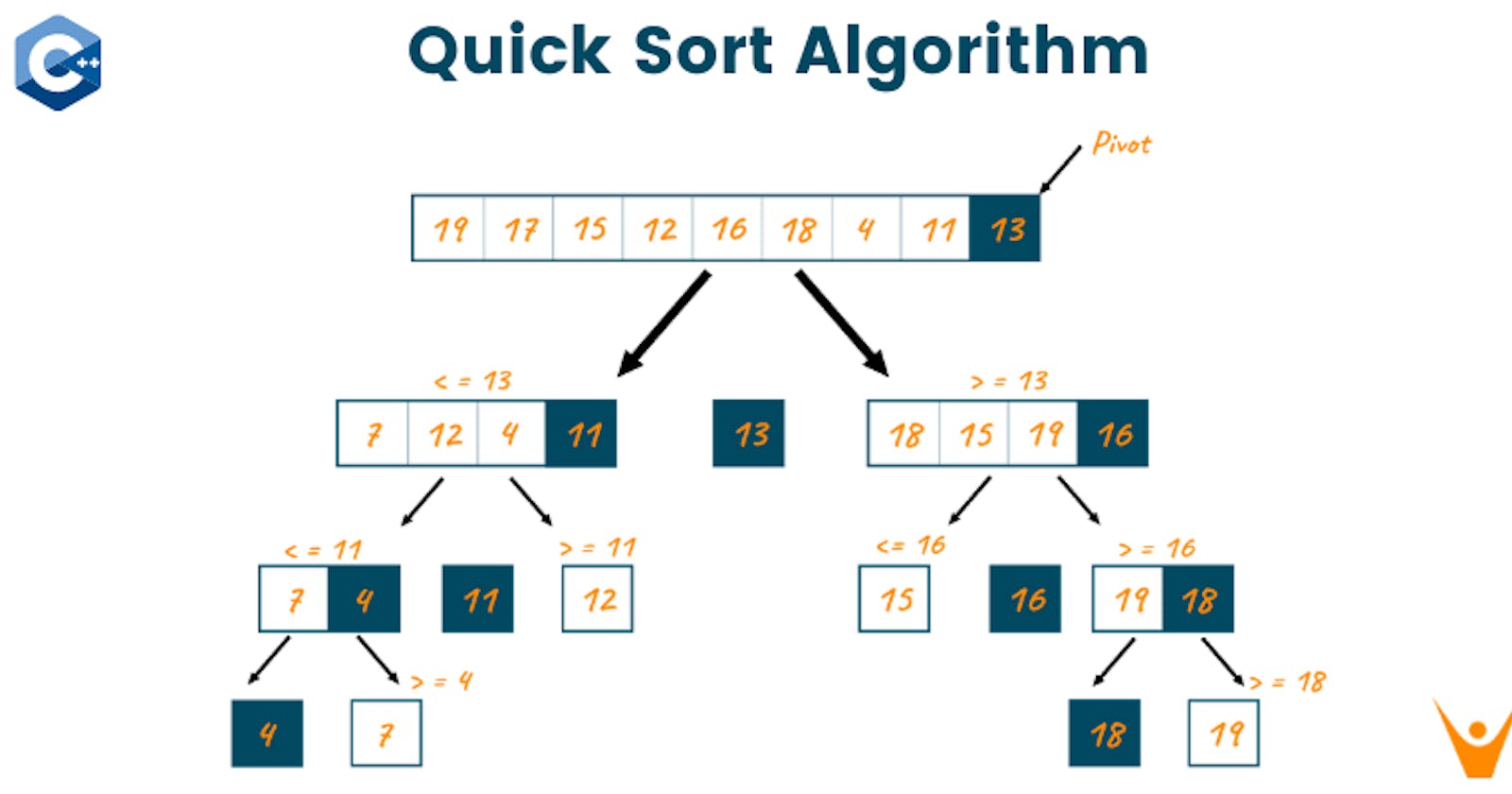
As a part of my 100-day Data Structures and Algorithms (DSA) challenge, I recently delved into Quick Sort, a popular sorting algorithm known for its efficiency and elegance in sorting arrays. Quick Sort follows the principle of 'divide and conquer,' efficiently breaking down the problem into smaller, more manageable parts to solve it.

The Quick Sort Algorithm

#include <bits/stdc++.h>
using namespace std;
//------------------Partition--------------------------//
int partition(int arr[],int s,int e){
    //consider the pivot element to be at start index
    int pivot_element = arr[s];
    //count the smaller element 
    int count = 0;
    for(int i =s+1;i<=e;i++){
        if(arr[i]<=pivot_element){
            count++;
        }
    }
    //pivot index would be s+count
    int pivot_index = s+count;
    swap(arr[pivot_index],arr[s]);
    //fullfill the 3rd condition <e | e| >e
    int i =s,j=e;
    while(i < pivot_index && j > pivot_index){
        while(arr[i]<arr[pivot_index]){
            i++;
        }
        while (arr[j]>arr[pivot_index]){
            j--;
        }
        if(i < pivot_index && j > pivot_index){
            swap(arr[i++],arr[j--]);

        }

    }
    return pivot_index;
}
//------------------Quick Sort-------------------------//
void quick_sort(int arr[],int s,int e){
    //base Case
    if(s>=e){
        return;
    }
    //partitioning
    int pivot = partition(arr,s,e);

    //sort the left part
    quick_sort(arr,s,pivot);
    //sort the right part
    quick_sort(arr,pivot+1,e);
}

int main(){
    int arr[5] = {3,1,4,5,2};
    int n = 5;
    quick_sort(arr,0,n-1);
    for(int e:arr){
        cout<<e<<" ";
    }
    return 0;
}

Let's dive into the code that I explored and dissected, understanding its working and significance in sorting.

The Partition Function

The partition function is the core of Quick Sort, responsible for rearranging elements around a pivot. Here's a simple breakdown of its steps:

1. Choosing a Pivot: The algorithm selects a pivot element (in this case, the first element of the array) to compare against.

2. Counting Smaller Elements: It counts the number of elements smaller than the pivot.

3. Rearranging Elements: It rearranges the elements such that all elements smaller than the pivot come before it, and larger elements come after it.

Quick Sort Function

The quick_sort function implements the recursive nature of the Quick Sort algorithm:

1. Base Case: It checks if the start index is greater than or equal to the end index. If so, it returns, as the array is already sorted.

2. Partitioning the Array: It utilizes the partition function to find the correct position of the pivot.

3. Sorting the Left and Right Parts: Recursively, it sorts the left and right portions of the array concerning the pivot, effectively dividing the problem into smaller sub-arrays until the entire array is sorted.

Sample Code Execution

In the main function, the Quick Sort algorithm is applied to an example array {3, 1, 4, 5, 2} of size 5. The sorted array is printed, demonstrating the effectiveness of the Quick Sort algorithm.

Understanding the Efficiency

Quick Sort is highly efficient, with an average time complexity of O(n log n). However, in its worst-case scenario, it can degrade to O(n^2) if the pivot selection is consistently poor. Despite this, its average-case efficiency and space complexity of O(log n) make it a favourable choice for sorting large datasets.

Conclusion

In conclusion, Quick Sort is a powerful and widely used sorting algorithm due to its simplicity, efficiency, and effectiveness in most scenarios. By dividing the problem and conquering it through recursive partitioning, Quick Sort stands as a testament to the effectiveness of divide-and-conquer strategies in algorithmic problem-solving.

Through my exploration and understanding of Quick Sort, I've gained insights into its inner workings, its efficiency, and its importance in the realm of sorting algorithms.